You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

题目描述

给定一棵 $n$ 个点的无根树，有 $q$ 次询问。

每次询问给一个参数三元组 $(a,b,c)$ ，求有多少个 $i$ 满足这棵树在以 $i$ 为根的情况下 $a$ 和 $b$ 的 LCA 为 $c$ 。

输入格式

第一行2个数，为 $n$ 和 $q$ 。

接下来 $n-1$ 行，每行 $2$ 个数，表示树的一条边。

接下来 $q$ 行，每行 $3$ 个数，为 $(a,b,c)$。

输出格式

共 $q$ 行，每行一个数，为对于每个三元组的 $i$ 的个数。

10 5
1 2
1 3
2 4
2 5
2 10
5 6
3 7
7 8
7 9
4 6 2
4 10 1
6 8 3
9 10 2
4 10 5

7
0
1
4
0

5 3
1 3
1 5
3 4
3 2
5 2 3
5 2 1
2 4 5

2
1
0

20 10
1 2
1 3
1 4
2 5
2 6
3 10
4 13
4 14
6 7
6 8
10 11
4 15
4 16
8 9
11 12
16 17
16 18
16 19
17 20
15 19 16
1 12 1
20 20 20
7 7 8
1 8 3
5 20 2
2 9 6
9 12 1
9 12 2
9 12 3

4
16
20
0
0
5
2
10
2
1

提示

---

样例2解释

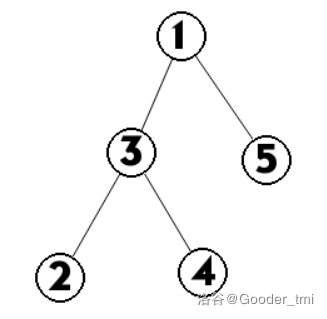
第一个查询的 $i$ 为 3 和 4。

第二个查询的 $i$ 为 1。

---

数据范围

本题按子任务测试：

$subtask1 (20pts)$：$1 \leq n \leq$ $1000$ ，$1 \leq q \leq$ $500$ 。

$subtask2 (15pts)$：$1 \leq n \leq$ $10^{5}$，$1 \leq q \leq$ $10^{5}$，树退化成链 。

$subtask3 (25pts)$：$1 \leq n \leq$ $5$ $\times$ $10^{5}$，$1 \leq q \leq$ $10^{5}$，数据不随机 。

$subtask4 (40pts)$：$1 \leq n \leq$ $5$ $\times$ $10^{5}$，$1 \leq q \leq$ $2$ $\times$ $10^{5}$ 。

对于所有数据：$1 \leq n \leq$ $5$ $\times$ $10^{5}$，$1 \leq q \leq$ $2$ $\times$ $10^{5}$ 。

注：数据强度不高，不必卡常与快读快输。