You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

题目描述

这个世界上一共有 $n$ 个国家，这些国家之间经常有贸易往来，于是为了方便，有 $m$ 条道路连接这些国家，每条道路连接两个国家，使得这两个国家之间可以轻松进行往来。

有了这些道路之后，商人在国家之间会赚取到更多的利润，所以为了限制商人的财富，国家之间制定了一个规则。商人经过每条道路，需要上交这条路对应的过路费 $w_i$，商人从起点国家到达目的地国家时，会返还给他走的路径上的过路费最大的那条路的费用 $\max w_i$ 减去过路费最小的那条路的费用 $\min w_i$。

现在，有 $k$ 个商人要从一号国家出发，去各个国家进行贸易，你需要计算他们每个人如何走可以使得他自己的过路费最少，你只需要告诉他们每个人这个最小过路费即可。

输入格式

第一行三个整数 $n, m, k$，分别表示国家的个数，道路的数量和商人的数量。国家的编号由 1 到 $n$。

接下来 $m$ 行每行三个整数 $u_i, v_i, w_i$，表示有一条连接 $u_i$ 号国家和 $v_i$ 号国家的道路，其过路费为 $w_i$。

接下来 $k$ 行每行一个整数 $t_i$，表示每个商人的目的地国家编号。

输出格式

输出共 $k$ 行，一行一个整数 $c_i$，表示第 $i$ 名商人要到达目的地所需要的最小花费。

5 4 4
5 3 4
2 1 1
3 2 2
2 4 2
2
3
4
5

1
2
2
4

6 8 5
3 1 1
3 6 2
5 4 2
4 2 2
6 1 1
5 2 1
3 2 3
1 5 4
2
3
4
5
6

2
1
4
3
1

提示

样例解释 1

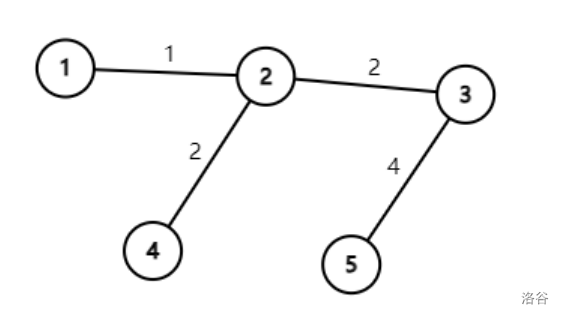
如上图。

• 对于路径 $1 \to 2$，花费为 $1 - 1 + 1 = 1$；
• 对于路径 $1 \to 3$，花费为 $1 + 2 - 2 + 1 = 2$；
• 对于路径 $1 \to 4$，花费为 $1 + 2 - 2 + 1 = 2$；
• 对于路径 $1 \to 5$，花费为 $1 + 2 + 4 - 4 + 1 = 4$；

数据范围

• 对于 $10\%$ 的数据，$n \leq 10$；
• 对于 $30\%$ 的数据，$n \leq 2 \times 10^3$；
• 对于另外 $20\%$ 的数据，$k = 1$；
• 对于另外 $10\%$ 的数据，$w_i$ 相同；
• 对于 $100\%$ 的数据，$1 \leq n \leq 2 \times 10^5, n - 1 \leq m \leq \min(\frac{n(n - 1)}{2}, 2 \times 10^5), 1 \leq k \leq n - 1, 0 \leq w_i \leq 10^9$，数据保证不存在重边和自环。