二分

• 二分的基础的用法是在单调序列或单调函数中进行查找
• 当问题的答案具有单调性时，就可以通过二分把求解转化为判定（根据复杂度理论，判定的难度小于求解）
• 三分法解决单峰函数的极值以及相关问题
• 二分的实现方法多种多样
  • 整数域上的二分，需要注意终止边界、左右区间取舍时的开闭情况，避免漏掉答案或造成死循环
  • 实数域上的二分，需要注意精度问题

整数集合上的二分

• 下面的写法保证最终答案处于闭区间 $[l,r]$ 以内，循环以 $l==r$ 结束，每次二分的中间值 $mid$ 会归属于左半段与右半段二者之一
• 循环都是以 $l == r$ 结束的

最大值最小

• 在单调递增序列 $a$ 中查找 $\geq x$ 的数中最小的一个（即 $x$ 或者 $x$ 的后继）

• while (l < r) {
  	int mid = (l + r) >> 1;
  	if (a[mid] >= x) r = mid;
  	else l  = mid + 1;
  }
  return a[l];
  

最小值最大

• 在单调递增序列 $a$ 中查找 $\leq x$ 的数中最大的一个（即 $x$ 或 $x$ 的前驱）

• while (l < r) {
  	int mid = (l + r + 1) >> 1;
  	if (a[mid] <= x) l = mid;
  	else r  = mid - 1;
  }
  return a[l];
  

细节点

• 两种形式

  • 最大值最小：$r = mid , l = mid +1 , mid = (l+r) >>1$
  • 最小值最大：$l = mid , r = mid -1 , mid = (l+r+1) >>1$
  • 如果不对 $mid$ 的取法加以区分，假如第二段代码也采用 $mid = (l+r)>>1$ , 那么当 $r-l$ 等于 $1$ 时，就有 $mid = (l+r)>>1 = l$
    • 若进入 $l = mid$ 分支，可行区间未缩小，造成死循环
    • 若进入 $r = mid -1$ 分支，造成 $l>r$ , 循环不能以 $l==r$ 结束

• 采用 **右移运算 $>> 1$ ** , 而不是 整数除法 $/2$

  • 右移运算是向下取整
  • 整数除法是向零取整，在包含负数时不能正常工作

• $mid$ 的取法

  • $mid = (l+r)>>1$ 不会取到 $r$ 这个值
  • $mid = (l+r+1)>>1$ 不会取到 $l$ 这个值
  • 利用这个特性来处理无解的情况，把最初的二分区间 $[1,n]$ 分别扩大为 $[1,n+1]$ （最大值最小） 和 $[0,n]$ （最小值最大）
    • 把 $a$ 数组的一个越界下标包含进来，如果最后二分终止于扩大后的这个越界下标上，则说明 $a$ 中不存在所求的数

• 这种整数域上的二分写法的优点是始终保持答案位于二分区间内，二分结束条件对应的值恰好在答案所处位置，还可以很自然地处理无解的情况，形式优美

  • 缺点是由两种形式共同组成，需要认真考虑实际问题选择对应的形式

实数域上的二分

• 实数域上二分较为简单，确定好所需的精度 $eps$ ，以及 $l + eps < r$ 为循环条件，每次根据在 $mid$ 上的判定选择 $r= mid$ 或 $l = mid$ 分支之一即可

• 一般需要保留 $k$ 位小数时 ， 则取 $eps = 10^{-(k+2)}$

• double eps = 1e-5;
  while (l + eps < r) {
  	double mid = (l + r) / 2;
  	if (check(mid)) r = mid;
  	else l = mid;
  }
  

• 有时精度不容易确定或表示，就干脆采用循环固定次数的二分方法，也是一种相当不错的策略。这种方法得到的结果的精度通常比设置 $eps$ 更高

• for (int i = 0; i < 100; i++) {
  	double mid = (l + r) / 2;
  	if (check(mid)) r = mid;
  	else l = mid;
  }
  

三分求单峰函数极值

• 单峰函数：拥有唯一的极大值点，在极大值点左侧严格单调上升，右侧严格单调下降

• 单谷函数：拥有唯一的极小值点，在极小值点左侧严格单调下降，右侧严格单调递增

• 通过三分法求其极值

• 以单峰函数为例，在函数定义域 $[l,r]$ 上任取两个点 $lmid$ 和 $rmid$ , 把函数分为三段

  • 若 $f(lmid) < f(rmid)$ , 则 $lmid$ 和 $rmid$ 要么同时处于极大值点左侧（单调上升函数段），要么处于极大值点两侧。无论哪种情况下，极大值点都在 $lmid$ 右侧，可令 $l= lmid$

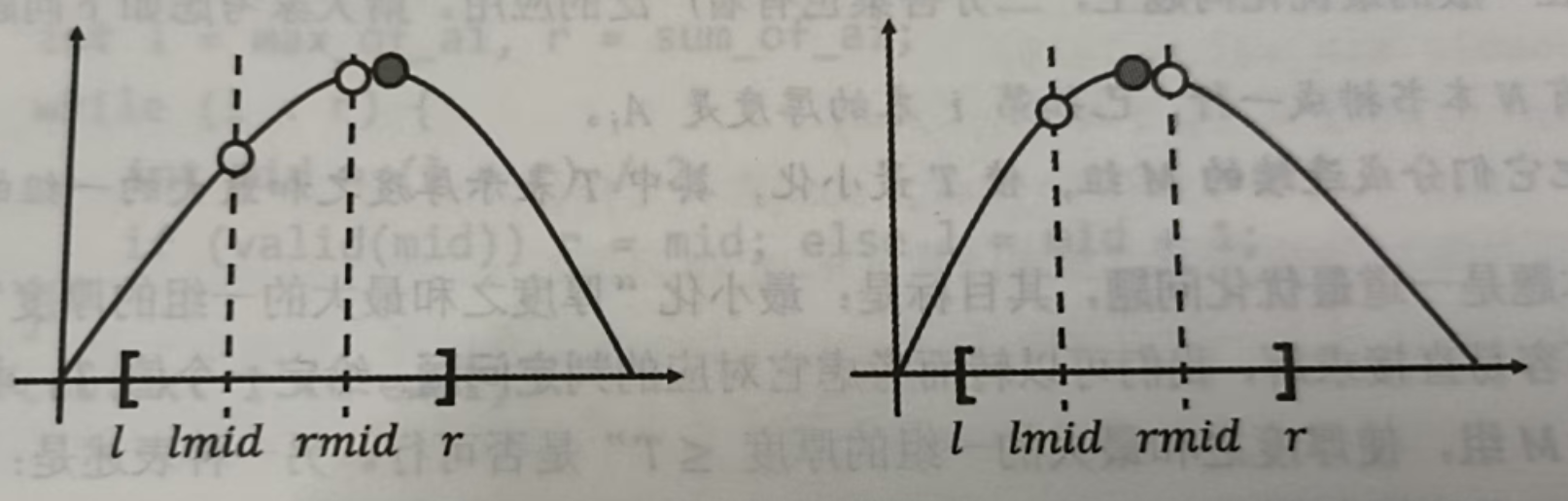
  • 若 $f(lmid) > f(rmid)$ , 则极大值点一定在 $rmid$ 左侧，可令 $r=rmid$

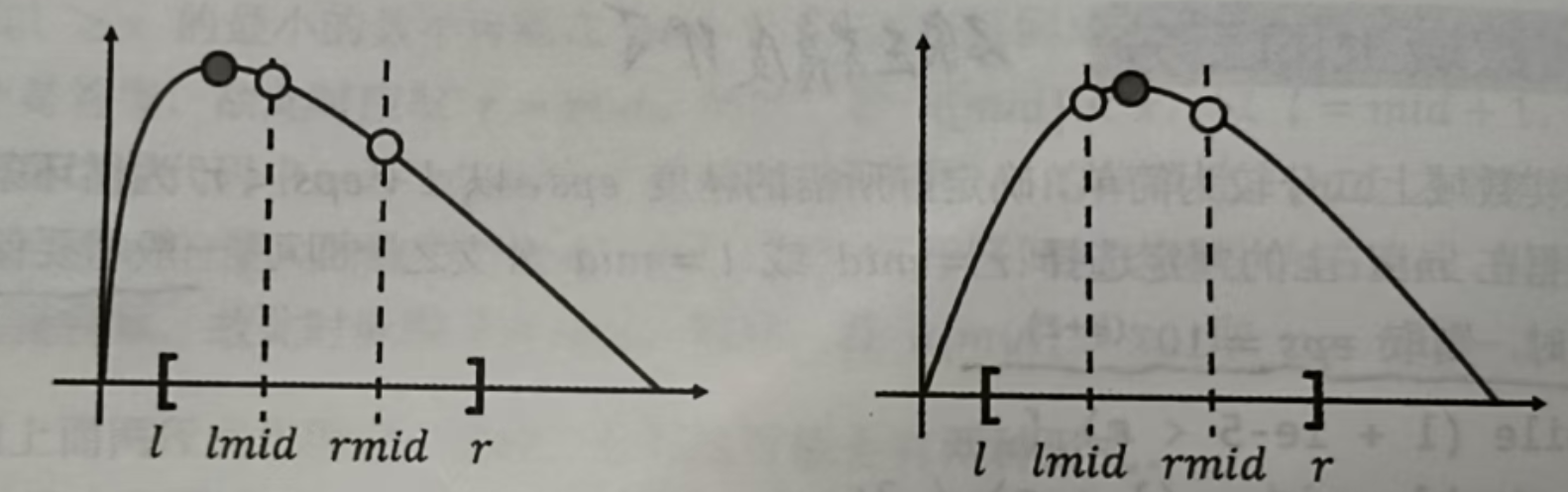
• 三分法只适用于 严格单调递增或者严格单调递减

  • 如果函数不严格单调，即在函数中存在一段值相等的地方，那么我们无法判断定义域的左右边界如何缩小，三分法不再适用